지도학습(Superviesed Learning)은 Input $x$를 넣었을 때 Output $y$값을 산출하는 것입니다. 다른 관점에서 생각해보면, $x$가 주어졌을 때 $y$ 값이 $y\prime$일 확률을 구하는 것으로 바꾸어 생각할 수 있습니다.
세상에는 다양한 문제 유형이 존재합니다. 이러한 문제 유형은 $y$의 분포(Distribution)에 따라 달라집니다. 개와 고양이를 분류해야 하는 이진 분류(Binary Classification)문제, 영화 리뷰를 분석하여 해당 영화가 어떤 카테고리에 속하는지 분류해야 하는 다중 분류(Multiclass Classification) 문제, 한 개 이상의 독립 변수 X와의 선형성을 판단하는 선형 회귀(Linear Regression)문제, Input 1개에 대한 여러 Output이 존재하는 경우 다항 회귀(Multimodel Linear Regression)문제로 판단합니다.
어떠한 $x$가 주어졌을 때 $y$에 속할 확률을 구하는 방법은 상기 문제의 종류에 따라 달라집니다.
- 이진 분류 : 베르누이 분포(Bernoulli Distribution)
- 다중 분류 : 카테고리 분포(Categorical Distribution)
- 선형 회귀 : 가우시안 분포(Gaussian Distribution)
- 다항 회귀 : 가우시안 믹스쳐(Mixture of Gaussians)
Important Distributions
Bernoulli Distributions
베르누이 분포는 이진 분류에서 사용되는 확률 추정 방법으로 $\mathcal{B}(\mu)$와 같이 나타내며, 수식으로는 다음과 같이 표현됩니다.
\[p(y|x) = \mu^y(1-\mu)^{1-y},\quad where\ y \in \{0, 1\},\quad \mu \in [0, 1]\]상기 수식에서 $if\ y=0$이면, $(1-\mu)$만 남게 되고, $if\ y=1$이면, $\mu$만 남게됩니다. 이진 분류 문제이기 때문에, 어느 하나의 값을 구하면 나머지 클래스에 대한 값도 자동적으로 추정됩니다. 산출된 값은 최종적으로 시그모이드 함수($\sigma$)를 통해 0과 1사이의 값으로 매핑됩니다. 값이 작으면 작을수록 0에 가깝게, 크면 클수록 1에 가깝게 매핑됩니다. 시그모이드 함수 수식은 다음과 같습니다.
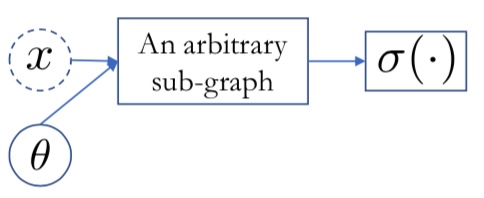
\[\sigma(a) = \frac{1}{1 + \exp(-a)}\]베르누이 분포에 대한 확률값을 추정하는 과정을 Graph로 표현하면 아래와 같습니다. Input $x$와 가중치와 같은 $\theta$ 값을 기반으로 Arbitrary한 Sub-graph를 구성합니다. Sub-graph 연산을 통해 산출된 값은 최종적으로 시그모이드 함수를 통해 0과 1사이의 값으로 매핑됩니다.
Categorial Distribution
베르누이 분포와는 다르게 카테고리 분포는 $y$의 클래스 개수가 3개 이상인 경우에 사용되며, $\mathcal C({\mu_1, \mu_2, \cdots, \mu_C})$와 같이 표현합니다. 카테고리 분포의 확률 추정은 다음과 같은 수식으로 표현됩니다.
\[p(y = v|x) = \mu_v, \quad where\ \sum_{v=1}^{\mathcal C} \mu_v= 1, \quad \mu = \begin{bmatrix} \mu_1 \\ \mu_2 \\ \cdots \\ \mu_C \end{bmatrix}\]$x$라는 input이 주어졌을 때, $y$의 $v$번 째 클래스에 속할 확률을 반환하는데, 그것을 $\mu_v$라고 정의합니다. 산출된 여러개의 $\mu$에 대한 확률 값을 산출하기 위해 소프트맥스 함수를 적용합니다. 이는 베르누이 분포에서 시그모이드 함수를 적용하여 0과 1사이의 값으로 매핑했던 것과 같은 맥락으로, 여러 개의 클래스에 대한 확률 값을 0과 1사이의 값으로 매핑합니다. 단, 모든 $\mu$들의 합은 1이 됩니다.
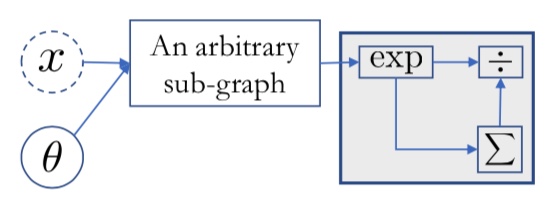
\[softmax(a) = \frac{1}{\sum_{v=1}^C \exp(a_v)} \exp(a)\]위와 같은 과정도 Graph로 표현할 수 있습니다. $x$라는 input값과 $\theta$를 정의하고, 이를 연산하기 위한 sub-graph를 정의합니다. sub-graph를 통해 산출된 값들은 소프트맥스 함수를 통해 정규화됩니다. 소프트맥스 함수를 적용하는 세부 과정은 산출된 $\mu$ 값들을 $\exp$ 연산을 통해 non-negative한 값으로 변환하여, 전체 $\mu$들을 더한 값으로 나누어 줍니다.
Gaussian Distribution
가우시안 분포는 회귀(Regression)에 사용되는 확률 추정 방법으로, Output의 클래스가 무수히 많은 때 사용하며 $\mathcal N(\mu, \mathbb{I})$로 표현합니다. 여기서 $\mathbb{I}$는 Identity Covariance를 의마합니다. 이에 대한 세부 수식은 아래와 같이 나타낼 수 있습니다.
\[p(y|x) = \frac{1}{Z} \exp(- \frac{1}{2}(y-\mu)^T (y-\mu))\]두 개의 차이가 얼마나 큰지 확인한 이후, 차이가 크면 확률값이 작아지고 차이가 작으면 확률값이 커지는 구조로 구성되어 있습니다.
Loss Function
인공신경망이 앞서 언급한 확률 추정 방법을 사용하여 최종적으로 확률값을 반환한다면, 이는 자연스럽게 Loss Function이라는 개념과 연결됩니다. 어떠한 모델이 Training을 진행하는 동안 지속적으로 높은 확률값을 반환한다면 이는 실제 데이터와의 Loss가 적다는 것을 의미하며, 이는 Loss값을 최소화 하는 방향으로 학습을 진행한다것과 일맥상통합니다.
다시 한 번 정리하면, 모델로 하여금 조건부 확률 분포가 훈련 샘플의 확률 분포와 같게 만드는 것, 즉 모든 훈련 샘플이 나올 확률을 최대화 하는 것(Loss값을 최소화 하는 것)을 Training이라고 할 수 있습니다. 이는 다음과 같은 수식으로 표현할 수 있습니다.
\[\arg\max_{\theta} \log{p_\theta}(D) = \arg \max_{\theta} \sum_{n=1}^N \log{p_\theta}(y_n | x_n)\]상기 수식은 모든 훈련 샘플이 나올 확률을 최대화 하는 방향으로 학습을 진행한 것으로 이를 최대가능도 방법(Maximum Likelihood Estimation) 이라고 합니다. 같은 의미에서, 이를 Loss Function 수식으로 바꾸어 보면 아래와 같은 수식으로 표현할 수 있습니다.
\[L(\theta) = \sum_{n=1}^{N}l(M_\theta(x_n), y_n) = -\sum_{n=1}^{N} \log{p_\theta (y_n | x_n)}\]이는 단순히 최대가능도 방법에 $-$를 취하여 만든 것입니다. 수식 중간에 $\log$가 들어가는데, 일반적으로 Probability를 추정할 때에는 $\log$ Probability를 추정한다고 생각하면 됩니다. 이는 여러가지 이유가 있으나, 추후에 설명드리겠습니다.
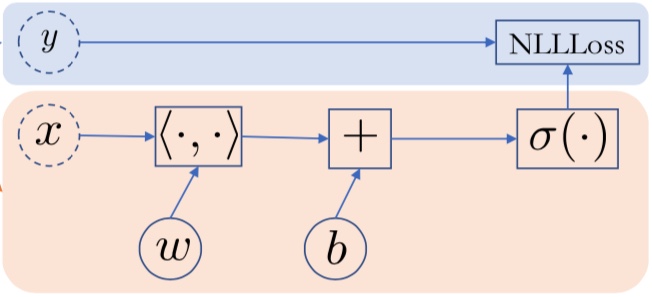
최종적으로, 모델의 학습 방향을 결정하기 위해 Graph의 맨 마지막 부분에 NLL(Negative Log Loss) Probability 노드를 추가하게 됩니다.
References
Machine Learning Basic의 모든 포스팅은 뉴욕대 조경현 교수님의 ‘딥러닝을 이용한 자연어 처리’ MOOC 강의를 정리한 것입니다. (https://www.edwith.org/deepnlp/joinLectures/17363)