앞선 포스팅에서 비순환그래프(DAG)를 설계하고, 각 Example들의 Loss값을 산출하기 위해 Loss Function을 정의하는 방법까지 알아보았습니다. 앞서 정의한 두 단계는 순차적으로 진행되며, 각 Example에 대한 Loss는 비순환그래프(DAG)를 거쳐 계산됩니다. 우리의 궁극적인 목표는 Loss를 최소화하는 모델을 찾는 것입니다. 다만, Loss를 구하기 위한 가설집합(Hypothesis Set)의 개수가 너무나 많기 때문에 모든 가설들을 전부 검증할 수 없다는 한계점이 존재합니다. 그렇다면, 주어진 랜덤 파라미터($\theta$)를 기반으로 어떻게 Loss($L$)를 최소화 할 수 있을까요?
How do we optimize the loss function?
위와 같은 한계점을 극복하기 위한 연구들은 오래전부터 진행되어 왔습니다. Iterative Optimization, Gradient Descent등과 같은 고전적인 최적화 방법부터 Adam Optimization, Ndam Optimization등 최근 발표된 알고리즘들이 존재합니다. 이러한 알고리즘들은 모두 Loss를 최소화한다는 공통적인 목표를 가지고 개발되었으 나, Loss의 최소 지점을 찾기 위한 세부적인 방법이 다르다고 할 수 있습니다. 이번 포스팅에서는 고전적인 최적화 알고리즘인 Iterative Optimization 방법과 Gradient Descent 방법에 대해 알아보겠습니다.
Iterative Optimization(Random Guided Search)
Iteratvie Optimization 방법은 1) 가설집합($\mathcal{H}$)에서 무작위로 하나의 가설을 선택하여, 2) 정규분포($\mathcal{N}(0, s^{2}1$))를 따르는 $k$개의 노이즈($\epsilon$)를 생성하여 연산을 진행합니다. 3) 최종적으로, $k$번의 연산을 진행하여 Loss가 가장 낮은 파라미터를 가지는 모델을 선택합니다. 4) 이러한 과정을 반복적으로 진행하여 최적의 모델을 찾습니다. 이러한 일련의 과정을 수식으로 표현하면 아래와 같습니다.
- Stochastically perturb $\ \theta_0 : \theta_k = \theta + \epsilon_k, \quad where\ \epsilon_k ~ \mathcal{N}(0, s^{2}1)$
- Test each perturbed point $\ L(\theta_k)$
- Find the best perturbed point $\ \theta_1 = \arg\min_{\theta_k}L(\theta_k)$
- Repeat this unitl no improvement could be made
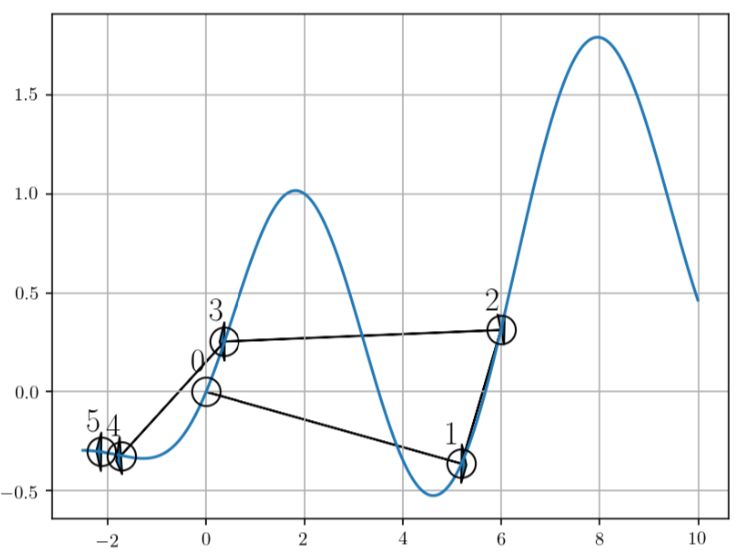
아래의 그래프는 $x$축이 Loss값이고, $y$값이 Random하게 선택된 파라미터입니다. 그래프를 살펴보면 최초 Random하게 선택된 Parameter에 의해 0번 지점이 선택되었습니다. 바로 다음 시도에서는 운이 좋게도 더 낮은 Loss값을 가지는 1번 지점이 선택된 것을 확인할 수 있습니다. Random한 노이즈를 기반으로 Loss를 측정하기 때문에 기존보다 더 낮은 Loss를 가지는 모델을 찾을 수도, 찾지 못할 수도 있습니다.
Pros
- 어떠한 비용함수를 사용하더라도 무관하다는 장점이 있습니다.
Cons
- 차원의 수가 적을 때는 잘 되지만, 차원이 커질수록 오래걸립니다.
- 샘플링(Sampling)에 따라서 오래걸릴 수 있습니다.
Gradient-based Optimization
Gradient-based Optimization 알고리즘은 Iteratvie Optimization 알고리즘과 동일하게 Random Point에서 시작합니다. 이후, Random Point의 미분을 통해 기울기(Gradient)를 계산합니다. 그래프의 최저점 방향으로 학습하는 것이 Loss를 최소화 하기 위한 방법이기 때문에, 기울기가 작아지는 방향($-\nabla L(\theta_0)$)으로 학습을 진행합니다. 기울기가 작아지는 방향으로 학습을 진행할 때에는 $\eta$만큼씩 이동하여 기울기를 측정하고, 해당 기울기가 움직이기 전의 기울기보다 작아졌는지 확인합니다. 이러한 과정을 반복적으로 진행하며 최적화를 진행합니다. 이를 수식으로 나타내면 아래와 같습니다.
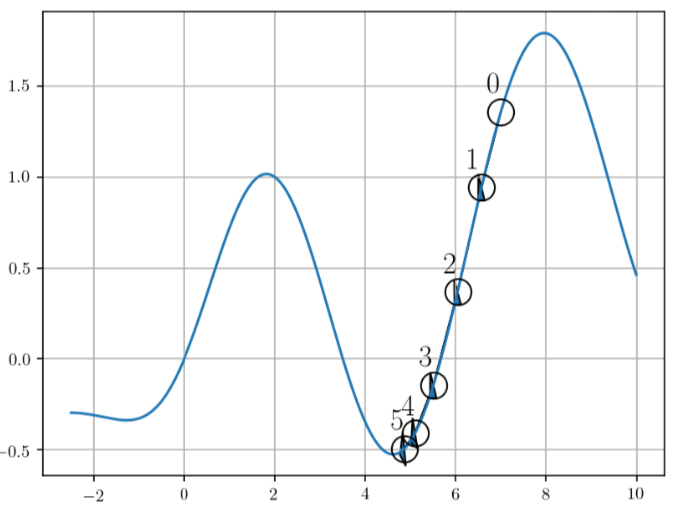
지금까지의 내용만 살펴보면 이상적인 최적화 방법이라고 할 수 있겠지만, 학습 과정의 Step 사이즈가 커지면 최저점을 지나칠 수 있다는 단점이 존재합니다. 아래의 그림은 순차적으로 기울기가 작아지는 방향으로 학습을 진행하고 있습니다. 0번째 Point에서 다음 포인트까지의 Learning Rate(Step Size)가 크다면, 5번째 Point를 지나쳐 다음 Convex로 넘어갈 수 있다는 위험 요소가 존재합니다.
Pros
- Random Guided Search에 비해서 탐색영역은 작지만, 확실한 학습 방향을 결정할 수 있습니다.
Cons
- 학습률(Learning Rate)가 너무 크거나 작으면 최적의 값을 지나칠 수 있습니다.
References
Machine Learning Basic의 모든 포스팅은 뉴욕대 조경현 교수님의 ‘딥러닝을 이용한 자연어 처리’ MOOC 강의를 정리한 것입니다. (https://www.edwith.org/deepnlp/joinLectures/17363)