Backpropagation은 네트워크 전체에 대해 반복적인 연쇄 법칙(Chain Rule)을 적용하여 Gradient를 계산하는 방법 중 하나입니다. 이번 포스팅에서는 주어진 함수 $f(x)$가 존재할 경우, 주어진 입력 $x$에 대해 함수 $f$의 Gradient($\nabla f(x)$)를 계산하는 것이 목표입니다. 신경망 관점에서 $f$는 손실 함수($L$)에 해당하고, 입력 $x$는 학습 데이터, 가중치(Weight), 바이어스(Bias) 등이 될 수 있습니다.
Gradient
$x$와 $y$ 두 숫자의 곱을 계산하여 반환하는 함수 $f$를 정의하면 $f(x, y) = xy$와 같이 표현할 수 있습니다. 각 입력 변수에 대한 편미분을 구해보면 아래와 같습니다.
\[f(x, y) = xy \quad \rightarrow \quad \frac{\partial f}{\partial x} = y \quad \frac{\partial f}{\partial y} = x\] \[\frac{df(x)}{d(x)} = \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\]위의 수식에서 $\frac{df(x)}{d(x)}$ 부분의 분수 기호는 나누기를 의미하지는 않습니다. $\frac{d}{dx}$가 함수 $f$에 적용되어 미분된 함수를 의미하도록 한 것입니다. 위의 수식이 의미하는 바는 $h$가 매우 작으면 함수 $f$는 직선으로 근사(Approximated)될 수 있고, 미분 값은 그 직선의 기울기를 의미합니다. 만약 $x = 4, y= -3$이면, $f(x, y) = -12$가 되고, $x$에 대한 편미분 값은 $x\frac{\partial f}{\partial x} = -3$으로 얻어집니다. 이는 $x$를 $h$만큼 증가시키면 전체 함수 값은 -3h만큼 변화한다는 것을 의미합니다.위의 수식을 재구성하면 다음과 같이 간단하게 표현할 수 있습니다.
\[f(x+h) = f(x) + h\frac{df(x)}{dx}\]Gradient($\nabla f$)는 편미분 값들의 벡터입니다. 수식으로 표현하면 다음과 같습니다.
\[\nabla f = \left[ \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right] = [y, x]\]아래와 같은 덧셈을 반환하는 수식에 대해서도 미분값을 산출할 수 있습니다.
\[f(x,y) = x + y \quad \rightarrow \quad \frac{\partial f}{\partial x} = 1 \quad \frac{\partial f}{\partial y} = 1\]$x, y$에 대한 미분은 $x, y$값에 관계 없이 1인 것을 확인할 수 있습니다. $x, y$값이 증가하면 $f$가 증가하기 때문입니다. 또한, $f$값의 증가율 또한 $x,y$값에 관계없이 일정한 것을 확인할 수 있습니다.
Chain Rule & Backpropagation
앞서 살펴본 $f(x, y) = xy$와 같이 간단한 표현식이 아닌 다수의 복합 함수를 가지는 표현식을 고려해보겠습니다. 함수 $f$가 $f(x,y,z) = (x+y)z$와 같이 정의될 때, 해당 식을 미분해보겠습니다. 미분하기 전, $x+y$를 $q$로 치환하면 $f = qz$로 나타낼 수 있습니다. 이러한 형태를 띄는 함수는 앞서 본 것 처럼 $q$와 $z$로 따로 구분하여 계산할 수 있음을 알 수 있습니다. 함수 $f$가 $q$와 $z$의 곱으로 구성되어 있기 때문에, 이를 $\frac{\partial f}{\partial z} = q, \frac{\partial f}{\partial q} = z$로 나타낼 수 있으며, 여기서 $q$는 $x$와 $y$의 합으로 구성되어 있기 때문에 이를 $\frac{\partial q}{\partial x} = 1, \frac{\partial q}{\partial y} = 1$로 계산할 수 있습니다. 연쇄 법칙(Chain Rule)은 이러한 Gradient 표현식들을 함께 연결시키는 적절한 방법이 곱셈이라는 것을 보여주고 있습니다. 아래는 이를 재현하기 위한 코드입니다.
# Set some inputs
x, y, z = -2, 5, -4
# Perform the forward computation
q = x + y # q becomes 3
f = q * z # f becomes -12
# Perform the backward computation(backpropagation) in reverse order
# First backpropagation through f = q * z
dfdz = q # df/dz = q, so gradient on z becomes 3
dfdq = z # df/dq = z, so gradient on q becomes -4
# backpropagation through q = x + y
dfdx = 1.0 * dfdq # dq/dx = 1.
dfdy = 1.0 * dfdq # dq/dy = 1결국 [dfdx, dfdy, dfdz] 변수들로 Gradient가 표현되는데, 이는 $f$에 대한 변수 x, y, z의 민감도를 보여줍니다. 이는 아래와 같은 그림으로 표현할 수 있습니다. Forward Computation(녹색)은 입력부터 출력까지 값을 계산합니다. 이후, Backward Computation(적색) 과정을 통해 Backpropagation을 수행합니다. 이 과정에서 반복적인 연쇄 법칙을 적용해 모든 노드의 Gradient를 계산합니다(Gradient 값은 거꾸로 계산되는 것을 확인할 수 있습니다).
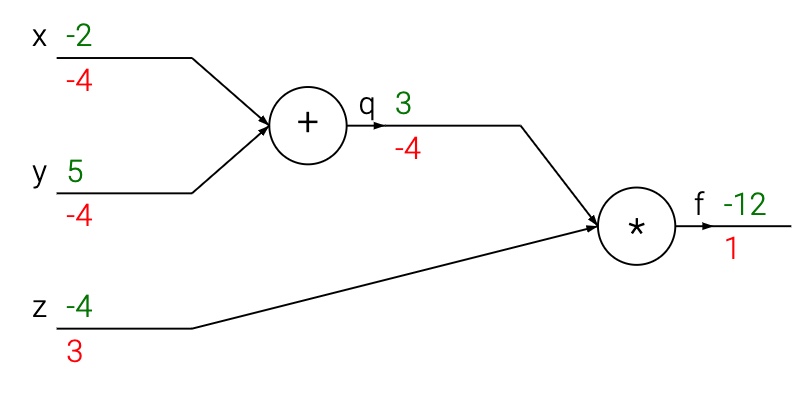
위의 그림에 대한 세부 프로세스는 다음과 같습니다. 덧셈 게이트는 [-2, 5]를 입력받아 3을 출력합니다. 이 게이트는 덧셈 연산을 진행하기 때문에 두 입력에 대한 지역적 Gradient는 1이 됩니다. 이후 3과 -4의 곱셈 연산을 통해 최종적으로 -12를 출력하게 됩니다. 연쇄 법칙을 통해 Backpropagation이 진행되는 동안, 덧셈 게이트는 출력 값에 대한 Gradient 값이 -4였음을 학습합니다. 만약 이 회로가 높은 값을 출력하기를 원한다면, 이 회로가 덧셈 게이트의 출력 값이 4의 힘만큼 낮아지길 원하는 것으로 볼 수 있습니다. 따라서, 반복을 지속하고 Gradient 값을 연결하기 위해 덧셈 게이트는 이 Gradient 값을 받아들이고 이를 모든 입력들에 대한 지역적 Gradient 값에 곱합니다. 만약 $x, y$가 감소한다면, 이 덧셈 게이트의 출력은 감소할 것이고 이는 다시 곱셈 게이트의 출력이 증가하도록 할 것입니다.
$\therefore$ Backpropagation은 보다 큰 최종 출력 값을 얻도록 게이트들이 자신들의 출력을 얼만큼 변화하길 원하는지 서로 소통할 수 있도록 합니다.
References
-
Backpropagation에 적용되는 Chain Rule과 Automatic Differentiation의 개념을 이해하기 위해 스탠포드 CS231n 강의 CS231n : Convolutional Neural Networks for Visual Recognition 의 강의노트를 정리한 포스트를 참고하였습니다. (http://aikorea.org/cs231n/optimization-2/)
-
Machine Learning Basic의 모든 포스팅은 뉴욕대 조경현 교수님의 ‘딥러닝을 이용한 자연어 처리’ MOOC 강의를 정리한 것입니다. (https://www.edwith.org/deepnlp/joinLectures/17363)