이전 포스팅에서 설명했던 것과 같이, 모델의 Loss값을 구하기 위한 방법들은 여러가지가 (i.e. Gradient Descent, L-BFGS, Conjugate Gradient $\cdots$) 있었습니다. 다만, 이러한 방법들은 데이터의 개수가 많아지고, Parameter가 많아질 수록 훈련 샘플 전체의 Loss를 구하기 위해 엄청난 시간과 리소스를 필요로 한다는 단점이 존재합니다. 훈련 샘플 전체의 Loss는 곧 각 Example들의 Loss의 합으로 구해지기 때문입니다. 이러한 한계점을 해결하기 위해, Stochastic Gradient Descent 방법이 고안되었습니다.
Stochastic Gradient Descent
위에서 설명한 바와 같이, Stochastic Gradient Descent(이하 SGD) 데이터셋이 커졌을 때 Loss를 구하기 위한 리소스를 최소화하기 위해 만들어진 알고리즘입니다. SGD는 훈련 샘플 전체의 Loss를 구하지 않고, 전체 샘플 중 일부만을 사용하여 훈련 샘플 전체의 Loss를 추정합니다.
\[\nabla{L} \approx \frac{1}{N'} \sum_{n=1}^{N'}{\nabla{l}(M(x_{n'}), y_{n'})}\]예를 들어, 전체 훈련 샘플의 개수가 1000개라면, 전체 데이터셋을 $N$개의 미니 배치(Minibatch)로 나누어 각 배치에 대한 Loss값을 산출합니다. 물론, 전체 훈련 샘플을 사용하여 계산한 Loss값보다 정확하다고 할 수는 없지만, 근사치에 해당하는 Loss값을 얻을 수 있습니다. SGD의 세부 프로세스는 아래와 같습니다.
1) Grab a random subset of $M$ training examples (Minibatch)
\[D' = \{ (x_1, y_1), \dots , (x_{n'}, y_{n'}) \}\]2) Compute the minibatch gradient
\[\nabla{L} \approx \frac{1}{N'} \sum_{n=1}^{N'}{\nabla{l}(M(x_{n'}), y_{n'})}\]3) Update the parameters
\[\theta \leftarrow \theta + \eta \nabla L(\theta;D')\]4) Repeat until the validation loss stops improving
Early Stopping
과적합이란, 모델이 학습 데이터를 과하게 학습하여 학습 데이터가 아닌 다른 데이터가 들어오면 제대로 분류하지 못하게 되는 상태를 의미합니다. 일반적으로 Training Set에 대한 Loss값은 감소하는 반면, Validation Set에 대한 Loss값이 상승할 때에 과적합이 일어나고 있다고 판단합니다.
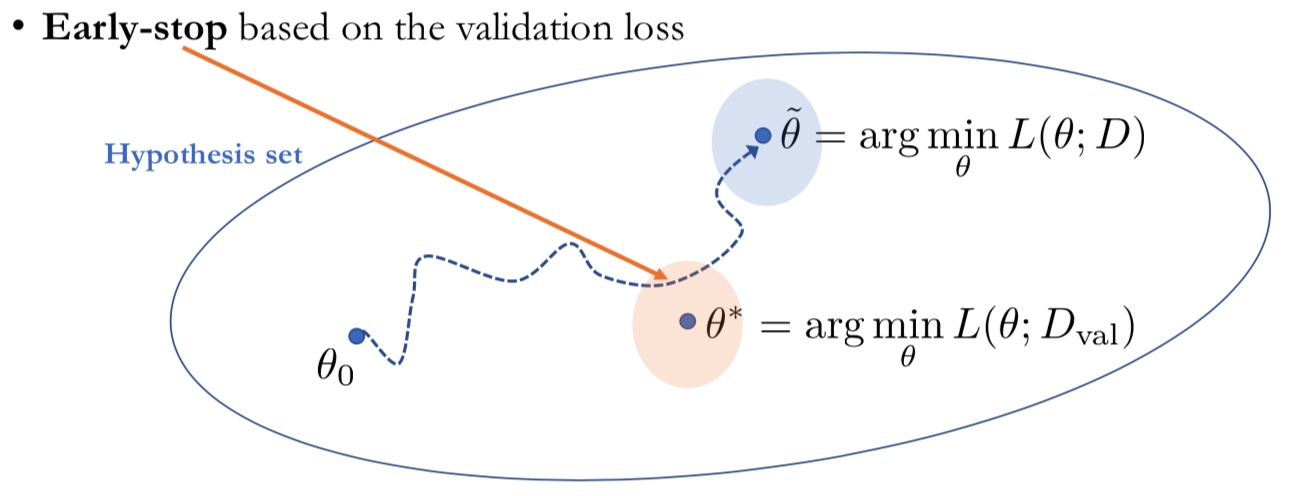
Early Stopping은 이러한 과적합(Overfitting) 방지를 위한 좋은 알고리즘입니다. 학습을 진행하는 과정에서 우리가 찾고자 하는 모델은 Training Set을 마지막까지 학습한 모델($\overset{\sim}{\theta}$)이 아닌, 학습 과정에서 Validation Set에 대한 Loss가 가장 낮은 모델($\theta^{*}$)입니다. Early Stop은 Validation Set의 Loss값을 지속적으로 체크하여, Loss가 가장 낮은 포인트에서 학습을 중단하도록 합니다.
Adaptive Optimization
Adaptive Optimization은 기존의 Stochastic Gradient Descent가 고정적인 Learning Rate를 가지고 학습을 진행하는 것을 보완하기 위해 고안되었습니다. 학습 과정에서 Learning Rate는 아주 중요한 역할을 하는데, 왜 중요한지 아래의 그림을 통해 확인해보겠습니다.
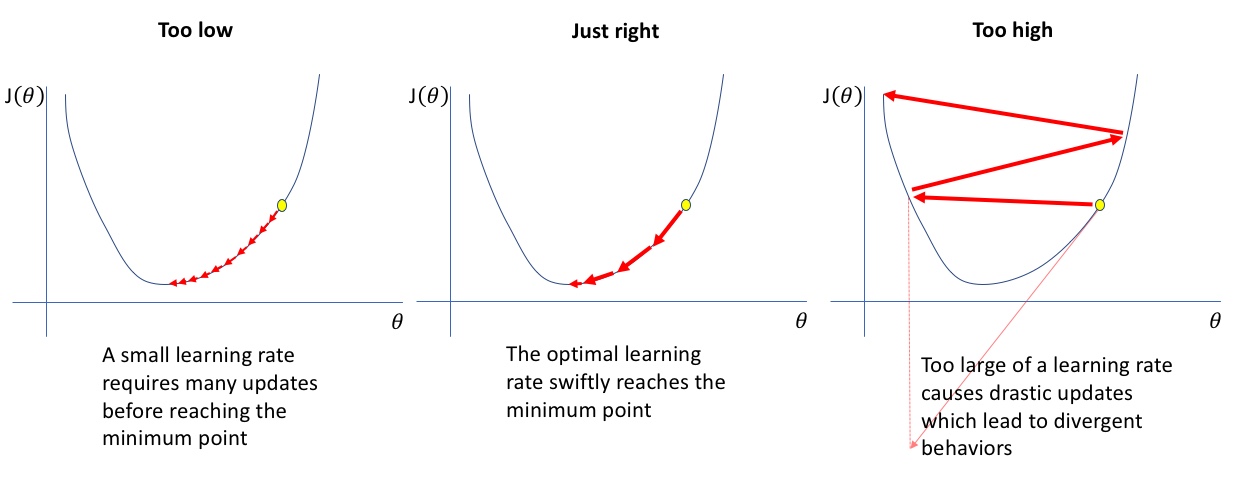
아래의 그림은 Learning Rate가 너무 작을 때, Adaptive할 때, 너무 높을 때를 순차적으로 표현하고 있습니다. Learning Rate가 너무 낮으면 정교한 학습이 가능하지만, 너무 많은 포인트에 대해 Loss값을 계산을 진행하기 때문에 학습 시간이 오래걸린다는 단점이 있습니다. 반면에, Learning Rate가 너무 높으면 빠른 학습이 가능하지만, 맨 오른쪽 그림과 같이 Saddle Point$^{\star}$를 건너 뛸 수 있다는 단점이 존재합니다. 이러한 한계점들을 보완하기 위해 고안된 것이 Adaptive Optimization 방법이며, 각 포인트의 Gradient를 계산하고, Gradient 변화량을 파악하여 Learning Rate를 조정하기 때문에 효과적으로 학습을 진행할 수 있습니다. Adaptive Optimization의 세부 프로세스는 아래와 같습니다. $^{\star}$ Saddle Point : Loss가 가장 낮은 지점
1) Grab a random subset of $M$ training examples (Minibatch)
\[D' = \{ (x_1, y_1), \dots , (x_{n'}, y_{n'}) \}\]2) Compute the minibatch gradient
\[\nabla{L} \approx \frac{1}{N'} \sum_{n=1}^{N'}{\nabla{l}(M(x_{n'}), y_{n'})}\]3) Update the per-parameter learning rate $\eta_\theta$
4) Update the parameters
\[\theta \leftarrow \theta - \eta_\theta \frac{\partial{L'}}{\partial{\theta}}\]5) Repeat until the validation loss stops improving
Adaptive Optimizer는 Adam Optimizer(Kingma&Ba, 2015), Adadelta(Zeiler, 2015) 등 여러 알고리즘들이 존재합니다.
References
Machine Learning Basic의 모든 포스팅은 뉴욕대 조경현 교수님의 ‘딥러닝을 이용한 자연어 처리’ MOOC 강의를 정리한 것입니다. (https://www.edwith.org/deepnlp/joinLectures/17363)