Survival Analysis. 카플란-마이어 추정 (Kaplan Meier Estimation)

Posted on | In

생존 분석(Survival Analysis)는 시간의 흐름에 따른 어떠한 사건의 발생 확률을 알아보는 통계 분석 및 예측 기법 중 하나입니다. 일반적으로 의료분야에서 특정 수술 방법 혹은 치료 방법에 따른 환자의 생존 기간을 분석할 때 활용하거나, 일반적인 IT 분야에서는 시간에 따른 사용자 이탈 분석에도 활용합니다. Survival Analysis에는 크게 3가지 주요 개념 사건(Event), 시간(Time), 중도절단(Censored)이 존재합니다.

  • 사건(Event) : 분야에 따라 사건의 정의가 달라지며, 사망 $\cdot$ 이탈 등이 사건에 해당합니다.
  • 시간(Time) : 대상을 관찰하기 시작한 시점으로부터 경과한 시간을 의미합니다.
  • 중도절단(Censored) : 중도절단은 Survival Analysis에서 손실된 데이터를 처리하기 위해 도입된 개념으로, Right Censored와 Left Censored로 구분됩니다.
    • Right Censored : 특정 사건이 발생한 시점이 특정 시기(연구가 끝난 시기) 이후인 경우
    • Left Censored : 특정 사건이 발생한 시점이 특정 시기(연구 기간)에 미치지 못한 경우

상기 3가지 기본 개념를 통해 생존 함수(Survival Function)과 위험 함수(Hazard Function)를 산출합니다.

  • 생존 함수(Survival Function) : 특정 시기보다 더 오래 생존할 확률을 추정합니다.
  • 위험 함수(Hazard Function) : 특정 시기에 사건이 발생할 확률을 추정합니다.

궁극적으로 3가지 기본 개념과 2가지 함수를 통해 생존 분석을 진행할 수 있습니다. 아래의 예제를 통해 상기 개념들이 어떻게 적용되는지 확인해보겠습니다.

Kaplan-Meier Estimation(Curve)

일반적으로 생존 함수는 Kaplan-Meier Estimation 방법을 통해 추정할 수 있습니다. 해당 방법은 적은 표본에 대해서도 적용할 수 있기 때문에 폭넓게 사용됩니다. Kaplan-Meier Estimation 방법을 통해 집단 간의 시간에 따른 생존율을 쉽게 비교할 수 있습니다.

Kaplan-Meier Estimation 방법은 전체 연구 기간 동안에 사건이 발생한 시점마다 구간생존율을 산출하여 최종적으로는 누적생존율을 산출합니다. 이 때문에 누적한계추정법(Product Limit Method)으로 불리기도 하며, 사건이 발생한 시점마다 생존율을 계산합니다. 사건의 관찰기간 순서대로 자료를 정렬한 뒤, 각 구간별로 관찰대상 수 중 생존자수의 비율로 구간생존율 $P(t)$를 산출합니다. 관찰기간동안 1명이 사망한 경우, 구간생존율은 $\frac{n-1}{n}$이 됩니다. 누적생존율 $S(t)$는 구간별 구간생존율을 차례대로 곱하여 산출할 수 있습니다. 구간생존율과 누적생존율의 세부 공식은 아래와 같습니다.

\[P(t) = \frac{t 시간까지의 생존자 수}{t 시간 까지의 관찰대상 수} \\ S(t) = S(t-1) \times P(t)\]

예제 데이터 생성

이해를 돕기 위해, 예제를 통해 어떻게 Kaplan-Meier Estimation 방법을 통해 생존율을 추정할 수 있는지 확인해보겠습니다.

import pandas as pd

data = pd.DataFrame({
    'time' : [2, 4, 6, 8, 10, 14, 18, 22, 28, 40],
    'event' : [True, True, True, True, True, False, False, True, True, False]
}, index = ['One', 'Two', 'Three', 'Four', 'Five', 'Six', 'Seven', 'Eight', 'Nine', 'Ten'])

data

먼저, 예제 데이터를 생성했습니다. 총 10개의 샘플에 대해 시간 및 사건 발생 여부를 입력하였습니다. 사건이 발생하면 True, 사건이 발생하지 않은 경우는 False로 표시하였습니다. 결과적으로 아래와 같이 데이터가 생성되었음을 확인할 수 있습니다.

IMAGE

Kaplan-Meier Curve 그리기

Python의 lifelines 라이브러리를 활용하면 Kaplan-Meier Curve를 그릴 수 있으며, Curve를 통해 특정 시점의 생존율을 추정할 수 있습니다.

from lifelines import KaplanMeierFitter

kmf = KaplanMeierFitter()
kmf.fit(data['time'], data['event'])

plot = kmf.plot_survival_function()
plot.set_xlabel('time')
plot.set_ylabel('S(t)')
plot

plot_survival_function() 함수를 통해 Kaplan-Meier 곡선을 그릴 수 있습니다. X축은 시간이며, Y축은 누적생존율 $S(t)$를 나타내도록 하였습니다.

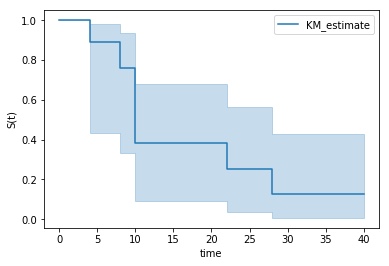
IMAGE

Kaplan-Meier Curve 해석

생성된 Kaplan Meier Curve를 통해 다양한 의사결정을 내릴 수 있습니다. 편의를 위해 시간의 단위는 월(Month)로 지칭하겠습니다.

1) 관찰 시작부터 관찰 종료 시점까지 점차 누적생존율이 떨어지는 것을 확인할 수 있습니다.

1) 관찰 시작 10개월이 지난 시점에 생존율이 급격하게 떨어지는 것을 확인할 수 있습니다.

1) 1년이 지난 시점에서의 생존율은 약 40%, 2년이 지난 시점에서의 생존율은 30% 정도로 추정할 수 있습니다.

이외에도 필요에 따라 여러 의사결정을 진행할 수 있습니다. 의료 분야에서는 특정 치료 방법 혹은 수술 방법이 환자의 생존 기간에 영향을 미치는 지 확인하기 위해 Kaplan-Meier 곡선을 활용합니다. 따라서, 본 예제에서 진행한 것과 다르게 기존 치료 방법과 새로운 치료 방법을 동시에 나타내어 어떠한 치료 방법이 높은 생존율을 가지는지 비교하기 위해 Kaplan-Meier 곡선을 사용하기도 합니다.